Encoders for the Nanotech World

By Reinhard Kuhn, Senior Project Manager, HEIDENHAIN, Traunreut, Germany

New encoder technology easily handles the measuring error due to guideway influences and thermal expansion, which at present can’t be compensated by computation, and overcomes some major hurdles to accurate measurement in the nanometer world.

Heidenhain’s LIF 481 1Dplus encoder that incorporates new measurement techniques meets the challenges of nanotechnology.

Nanotechnology refers to a number of technologies that involve structures and processes in the nanometer range (or a billionth of a meter: 10^-9 m) and denotes a limit range in which quantum physical effects begin to play an important role. The trend in the semiconductor industry, for example, to reach higher levels of integration and continuously finer structures, calls for measuring devices with higher resolution for positioning to the nanometer in manufacturing processes and in measuring and inspection technology. For semiconductor and other applications, such as optical manufacturing, the machines as well as measuring and testing equipment demand high positioning accuracy and repeatability, with values in the range of 100 nm to 1 nm and smaller.

The encoders in these machines are subject to stringent requirements for signal quality and accuracy. Currently, these requirements are met by laser interferometers or interferential optical encoders as position-measuring devices. Both offer resolutions well below 1 nm. Laser interferometers can be simply aligned with the tool center to eliminate Abbe error, or sine error, which is an amplification of angular error.

One of the drawbacks of these devices, however, is the dependency of the wavelength of laser light on environmental parameters such as temperature and air pressure. These parameters must be carefully measured along the interferometer’s optical path and the error must be continuously compensated. Any small fluctuation of the temperature, air pressure, or the composition of air and similar parameters ultimately changes the wavelength of the light and leads to position fluctuations on the order of 50 nm over a measuring length of 500 mm. The alignment error of the laser, which changes over time, leads to cosine or Abbe error that must be calibrated continuously.

With the appropriate arrangement of two or three scanning heads, the LIF 481 1Dplus linear encoder makes it possible to measure and compensate for both linear and angular guiding error as well as the influences of thermal expansion.

More stable measuring standards normally have a defined thermal behavior and are independent of air pressure fluctuations. For instance, the interferential scanning principle exploits the diffraction and interference of light on a fine graduation to produce signals used to measure displacement that are insensitive to air fluctuations. It works this way: A relative motion of the scanning reticle to the scale causes the diffracted wave fronts to undergo a phase shift. When the grating moves by one period, the wave front of the first order is displaced by one wavelength in the positive direction, and the wavelength of diffraction order –1 is displaced by one wavelength in the negative direction. Since the two waves interfere with each other when exiting the grating, the waves are shifted relative to each other by two wavelengths.

This arrangement results in two signal periods from the relative motion of just one grating period. So, for instance, interferential encoders function with grating periods of 8 or 4 µm, or even finer. Their scanning signals are largely free of harmonics and can be highly interpolated. These encoders are especially suited for high resolution and accuracy and have a high inherent repeatability. And their generous mounting tolerances permit installation in a range of applications.

New encoders, such as the LIF 481 1Dplus from HEIDENHAIN, incorporate these new measurement techniques. Besides the longitudinal track (x-axis) with interferential graduation and reference mark, the LIF 481 1Dplus features an additional y-axis track perpendicular to it. The absolute position on the scale, established by the reference mark on the x-axis, is gated with exactly one measuring step. A glass-ceramic reference standard, whose expansion coefficient of 0 +/− 0.1 x 10^-6/K^-1 is exact over a large temperature range and has a high resistance to aging, is used in the graduation carrier.

TEST SETUP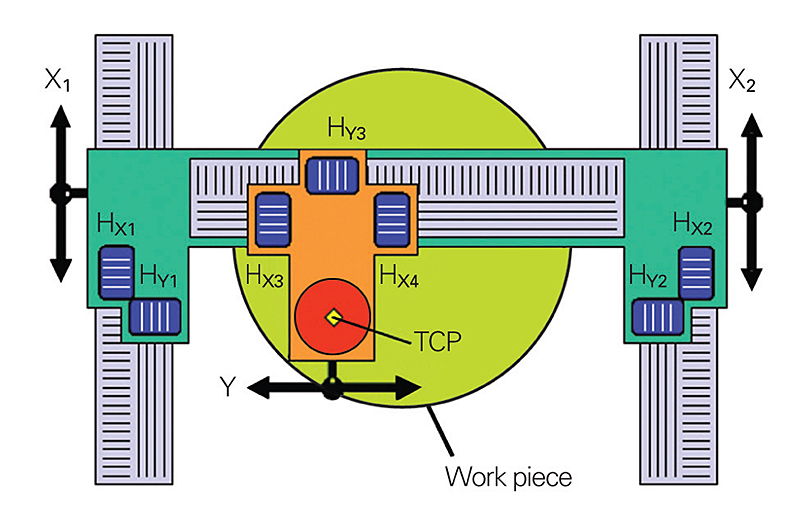

Here is an example of an LIF 481 1Dplus encoder used on a gantry-type milling machine.

The X-axis is equipped with two heads, HX1 and HX2, in an example arrangement of the scales. If the tool center point (TCP) is also aligned in Z to the centers of rotation HX1 and
HX2, all Abbe offsets of the X-axis are equal to zero. The heads HY1 and HY2 detect straightness error (y) of the X guideway axis and, to an extent, the influences of thermal
expansion. On the Y-axis the heads HX3 and HX4 can be used for compensation of straightness errors in the X-axis and Abbe error in the X-axis.

The Impact of Temperature and Guiding Error
The influence of guiding error and thermal changes presents significant challenges to nanometer-exact positioning within manufacturing processes and in measurement and testing metrology. Temperature fluctuations are true spoilsports for accuracy and reproducibility of measuring and testing technology. Under temperature fluctuation, the accuracy of the system remains limited in spite of expensive designs and materials or additional measures such as active cooling. Thermally induced geometrical changes of the machine can be mathematically compensated, although with some limitations.

The value of temperature measurement by sensor for linear compensation of thermally induced expansion depends on a number of factors including the quality of the sensors used, the correct placement (for example, with inhomogeneous temperature distribution), and the aging of the sensors. In addition, calibrated temperature sensors must be continuously monitored and, if required, replaced with sensors with the same properties.

Another factor comes from some system components themselves. For example, linear motors are also sources of heat, especially on fast machines, and can cause thermomechanical deviations. Because of their complex designs, gantry axes require special examination in this regard.

The graph shows the effect of incremental heating both with and without thermal compensation on Y-axis deviation.

Another factor is guiding error. All linear bearings have angular guiding error (pitch, yaw and roll) and linear guiding error (straightness, flatness). The error typically lies in the range of 5 to 100 µrad, or 0.5 to 5 µm. The relevant statistical dispersion of this error is only a fraction of these values and is very small for air bearings. Angular guiding error leads to local tilting and, with an Abbe offset other than zero, to a length offset of the encoder and thereby influences the machine accuracy.

Discuss this on the Engineering Exchange: