The length of a V-belt can be specified in several ways, including outside length, effective length, and pitch (or datum) length. Outside length is measured around the belt’s outer diameter with no tension, but is only an approximation and is not useful for sizing or selection. Effective length is measured at the effective outside diameter of the sheaves (pulleys), which is the location on the sheave where the groove’s top width is measured. Alternatively, the pitch length is measured at the pitch diameter of the sheaves. Both effective length and pitch length are measured with the belt tensioned by a specified amount.
Pitch length vs datum length

Improvements in belt design have moved the tensile cord to a position higher in the belt cross-section.
Image credit: Gates Corporation
Pitch length is difficult to measure directly, primarily because it is based on the pitch line of the belt. According to ISO 1081:2013, the pitch line is “any circumferential line which keeps the same length when the belt is bent perpendicularly to its base.” In other words, the pitch line is the line internal to the belt that does not change length when the belt is in use. The diameter that is formed on the sheave by the pitch line of the belt is the sheave’s pitch diameter.
A belt’s pitch line typically corresponds to the location of its internal tensile cord. But improvements in belt construction have moved the tensile cord to a location higher in the belt. This resulted in changes to the belt’s pitch length, and in turn, to the sheave’s pitch diameter. (This design change gives the tensile cord a larger moment arm and more support below it for transmitting forces to the sheave walls.)
In order to accommodate the changes in belt pitch length, and thus, sheave pitch diameter, the datum system was introduced. For most belts and sheaves, the dimensions formerly referred to as pitch length (belts) and pitch diameter (sheaves) are now referred to as datum length and datum diameter. In terms of sheave dimensions, the pitch diameter is now equal to the outer diameter for most standard sheaves. The datum diameter, however, is slightly less than the outer diameter. This is important when calculating the length of a belt, because the datum length, which is the norm for standard V-belt measurements today, is based on the datum diameter of the sheave. In contrast, the formerly used pitch length calculation was based on the sheave’s pitch diameter.
How to calculate datum length
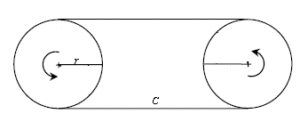
Case 1: Pulleys with equal diameters
Belt length is based on two factors: the center-to-center distance between pulleys and the arc of contact between the belt and the pulleys, which depends on the relative pulley diameters.
When the belt’s only purpose is to transmit power, pulleys of equal diameter are used on each end of the belt. In this case, the arc of contact is 180 degrees on each pulley. This means that the belt has contact with exactly one-half of circumference of each pulley, or the equivalent of one full pulley circumference. In order to determine the belt datum length, simply add the pulley circumference to twice the center distance between the pulleys.
![]()
Case 2: Pulleys with unequal diameters
When the belt is used to reduce speed or multiply torque, pulleys of different diameters are used. When the pulley diameters differ, the arc of contact is less than 180 degrees on the smaller pulley and greater than 180 degrees on the larger pulley. In this case, the formula for belt datum length requires determining the arc of contact on each pulley, as well as the length of belt between pulleys on both the top and bottom.
![]()
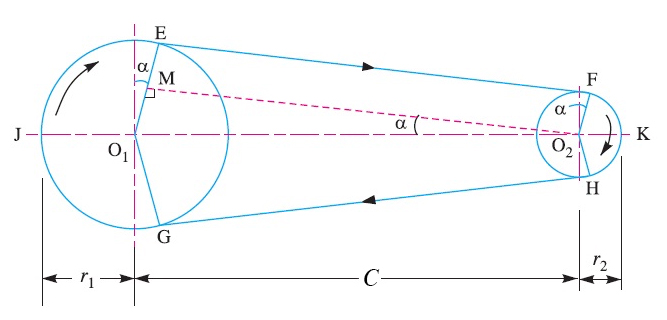
As shown in the figure, arc GJE is greater than 180 degrees, and arc FKH is less than 180 degrees, as determined by the angle α, or more specifically, by the sine of α, which is given as:
![]()
The arc GJE equals half of the larger sheave circumference, plus twice the length given by sin α:
![]()
Similarly, the arc FKH equals half of the smaller sheave circumference, minus twice the length given by sin α:
![]()
Note that MO2 is equal in length to EF and GH, so we can solve for MO2 to determine the length of belt between the pulleys. Using the Pythagorean theorem, we get:
![]()
Which can be expressed as:
![]()
Adding arcGJE, arcFKH, and twice the length EF (for the belt between pulleys on both top and bottom), gives:
![]()
Or, in terms of diameter:
![]()
Feature image credit: Frank Dorenberg
Filed Under: Linear Motion Tips, Motion control • motor controls




Tell Us What You Think!