Electrical resistivity (specific electrical resistance) and electrical conductivity (specific electrical conductance) are not at all the same as resistance and conductance. They are intrinsic properties that quantify the degrees to which various materials oppose or permit the flow of electric current. Glass, for example, has high resistivity and low conductivity, but it would be meaningless to say that it has high or low resistance or conductance unless the length and diameter were specified.
Resistivity is represented by the lower-case Greek letter Rho, ρ. The SI unit is ohms-per-meter. Conductivity is represented by the lower-case Greek letter Sigma, σ. The SI unit is Siemens-per-meter.
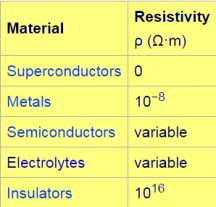 All materials have their own unvarying resistivities and conductivities, regardless of dimensions but subject to moisture content and the like. In contrast, a long thin wire of a given material has higher resistance and lower conductance than a short thick wire of the same material.
All materials have their own unvarying resistivities and conductivities, regardless of dimensions but subject to moisture content and the like. In contrast, a long thin wire of a given material has higher resistance and lower conductance than a short thick wire of the same material.
What makes for high conductivity? To answer this question we must consider band theory. Electrons orbit the nucleus at discrete distances or, more properly, energy levels. They are not like planets orbiting the sun, which may be at any distance. Moreover, unlike planets, whose orbits all lie approximately in the same plane, the electrons occupy three-dimensional shells.
According to quantum mechanics, electrons occupy discrete energy levels that are close together, forming energy bands. Electrons have a strong tendency to drop down to the lowest possible energy level, closer to the nucleus. The Pauli exclusion principle, however, predicts they cannot all go down to the lowest energy level. Each energy level has a specific number of electrons that it can contain, and these inner levels under ordinary conditions maintain just this number.
The outermost filled energy level is known as the Fermi level. Electrons close to the Fermi level have a tendency to jump around among energy levels, which are only partially occupied and thus have vacancies.
In metals, there is a great amount of this activity, and that is what accounts for the high conductivity. The electrons in the outer shell easily break their bonds and travel to other regions of the metal. This makes possible electric current. When a voltage is applied to a metal conductor in series with a suitable load, the electrons, repelled from the negative pole and attracted to the positive pole, move along the conductor to establish an electrical current. The actual electrons travel quite slowly, on the order of one meter per hour. However, since the electrons are densely packed, the applied voltage causes impulses to travel through the conductor at the speed of light, and that is what powers our civilization.
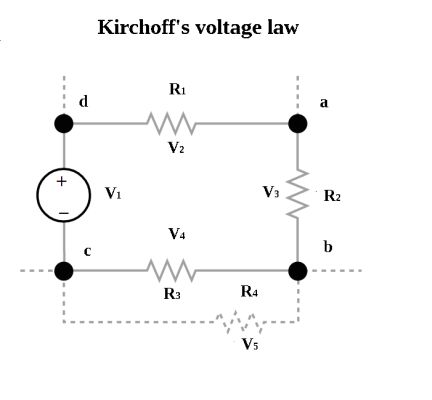
Kirchhoff’s voltage law simply says the sum of all voltages around a loop is equal to zero. Here,
v1 + v2 + v3 – v4 = 0
Of course, resistivity and conductivity enter into Ohm’s law which, together with Gustav Kirchhoff’s circuit laws, make it possible analyze lumped circuits. Kirchhoff’s theorem in the field of graph theory is known as his Matrix Tree theorem. To understand what is going on here, we have to begin by looking at matrix theory prior to his innovation. A matrix consists of a rectangular array of entries in rows and columns surrounded on either side by the characteristic brackets that signify that the numbers, symbols or expressions can undergo operations on a one to one basis such as addition and subtraction. There are various rules that govern when and if operations can be performed on a pair of matrices. For example, multiplication is allowed when the number of columns in the first matrix equals the number of rows in the second matrix. Kirchhoff extended the use of Laplacean matrix theory, making it applicable to contemporary search engine technology.
While Ohm’s law is capable of solving for voltage, current or resistance in all cases, the computation quickly becomes overwhelming when there are multiple branches with two or more power sources or a proliferation of three-dimensional networks. Kirchhoff’s laws (in the realm of mathematics they are called theorems) simplify circuit analysis and provide an intuitive basis that is essential in troubleshooting tough-dog problems.
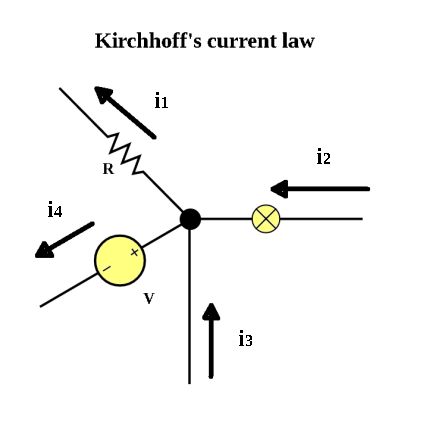
Kirchhoff’s current law simply says the current entering any junction equals the current leaving it. Here, i2 + i3 = i1 + i4
Kirchhoff’s Current and Voltage laws, known respectively as KCL and KVL, are easily stated. KCL states that from the principle of conservation of electric charge it follows that at any circuit node total current into that junction equals total current out. KVL states that from the principle of conservation of energy it follows that total electromagnetic force in any closed circuit is equal to total voltage drops in that loop.
Charge and energy are both subject to similar laws of conservation. In looking at an electrical circuit one always knows that these same values are either maintained in the circuit or exit by way of heat dissipation or magnetism, both measurable in the real world.
The post Resistivity, conductivity, and Kirchhoff’s laws appeared first on Test & Measurement Tips.
Filed Under: Flanges • supports • mounts • brackets, Test & Measurement Tips