By Ionut Ghionea, Lecturer, Faculty of Engineering University Politehnica of Bucharest
The finite element method (FEM) is one of the most used methods in engineering. This method and the programs based on it are fundamental tools in CAD usage. FEM/FEA are indispensable in all engineering analysis where high performance is required. The main purpose of this report is to present a practical application using FEA to improve design of a typical mechanical component.
Basics concepts of FEM/FEA
One of the major advantages in the finite element method is the simplicity of its basic concepts. To perform a finite element analysis, the user must develop a calculus model of the analyzed structure. There are no algorithms and general methods for developing a unique model that approximates, with a known error, the real structure. So several different models, all correct but with different performances, are generally used for the same structure. The development of a model is based on the intuition, experience and imagination of the user. Each model should incorporate all available information about the analyzed structure.
Each model consists of lines, planes or curved surfaces and volumes, created in a 3D CAD environment. In this stage of development, the model is continuous, with an infinite number of points, like the real structure. The main goal of FEM is to obtain the finite element mesh, transforming the continuous structure into a discrete model, with a finite number of points.
This operation is done using a mesh for the model, creating enough points inside the structure to characterize its mechanical behavior. The FEM defines the unknowns that are sought only in the nodes of the model and calculates their values in these points. Meshing must be done so as to have a number of nodes large enough to achieve a satisfactory approximation for the boundary and loading conditions. Thus, the mesh of the structure has a major importance in the FEM analysis.
The points defined in the mesh are called nodes. The primary unknowns of FEM are defined in nodes, and their values are the analysis results. These unknowns identified in the nodes can be displacements (displacement model) or stresses (stress model). For the displacement model, the deformed shape of the structure under a certain loading case is defined by the displacements of all the nodes with respect to the initial node net. Each node may have a maximum of six components of the displacement, called nodal displacements in a coordinate system: three linear displacements and three rotations. Some nodes are constrained and thus their displacements are zero or known by imposed values, so they should not be calculated anymore.
The meshing process divides the model into a certain number of quadrilateral or triangular fragments, called finite elements. These elements are assembled together in common nodes, also called vertices. In FEM, you study the finite element as a single piece in interaction with the other elements only in nodes. Thus, the study of the real structure is replaced with the study of the ensemble of finite elements obtained by meshing, in an idealization of the real structure. The finite elements must be designed in all details: geometrical, mechanical, or mathematical. This can be a difficult task, but most modern CAD-CAE systems are automatically resolving it with a little intervention from the user. The mesh of a structure can include elements defined for different types of analysis: linear elastic, nonlinear, heat transfer, fluid mechanics, or electromagnetic.
FEA/FEM advantages and limitations
Advantages include:
• General use — this is a numerical method used for solving problems in mechanics of deformable bodies, fluid mechanics, heat transfer, or biomechanics. The loading case can be static, dynamic, nonlinear, time-dependent.
• Litheness — to solve a problem, the user is free to elaborate the calculus model to meet his requirements. After this elaboration, often it is very simple to modify it, the goal being to get an enhanced variant of the initial model.
• Simplicity of the basic concepts — The method doesn’t require the user to possess good knowledge of mathematics, just an engineering background. The basic concepts, presented above, are easy to understand for correct use.
• Existence of FEM computer programs — FEA requires a huge amount of numerical calculations, almost impossible to perform manually. For this reason, many CAD-CAE systems include procedures for FEM calculations. Also, there are excellent FEM specialized programs available.
• Pre- and post processing facilities — The computer programs reduce time and effort, thus enabling automatic meshing and verification of the model. The results obtained from the FEM can be presented as images, tables, listings, drawings, diagrams, or animations.
Disadvantages include:
• The method is approximate — the analysis is not performed on a real structure, but on a model of it. All the results (such as stresses, strains, or displacements) are approximated and the user cannot precisely estimate the difference between the obtained results and the real ones.
• The calculus model is subjective and arbitrary — the user is free to elaborate the model without restrictions, but cannot be sure about the correctness of the model, or about the efficiency of the analysis that uses it. Sometimes, it is a good practice to validate the results by experiments on real structures.
• The FEA programs are complex and costly — the available FEM programs are very complex, with many options and capabilities.
A practical application of FEM
This application shows a FEM analysis of a support clamp, figure 1.
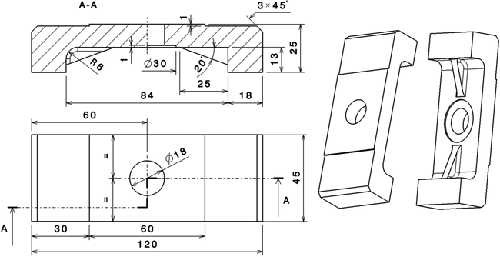
Fig. 1 — Support clamp (all dimensions in mm)
The analysis uses the CATIA program. After the solid modeling in the CATIA Part Design module, the user defines a material (steel), having the following physical characteristics: Young modulus (2_1011 N/m2), Poisson ratio (0.266), density (7,860 kg/m3) and yield strength (2.5_108 N/m2). Next, in the CATIA Generative Structural Analysis, the user establishes a Static-Case analysis and defines the node and finite-element net, in a process called discretization. In this process it is highly recommended to edit the default net parameters, defining the new finite-element size (5 mm) and type (linear), the absolute sag (1,25 mm) between the model and the real part, etc. To do this, the user must double-click the subelement “OCTREE Tetrahedron Mesh”, found in the specification tree, as shown in figure 2:
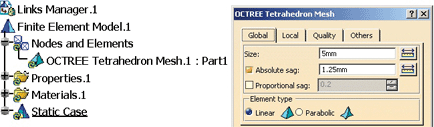
Fig. 2— The discretization process of the part.
Next, the part is constrained, figure 3.

Fig. 3— The application of the Clamp constraints.
The specification tree is completed with the subelement “Clamp.1”. The dialog window contains in the “Supports” field two faces, marked on the part model. On the part’s superior and functional surface, a 3000-N distributed force is applied perpendicular to the surface, in the opposite direction of Z axis. The specification tree shows the subelement “Distributed Force.1”. The force is symbolized by four arrows on the surface, its value and orientation, and the coordinate system where it was created; all these parameters can be specified in the corresponding fields of the dialog window, figure 4.
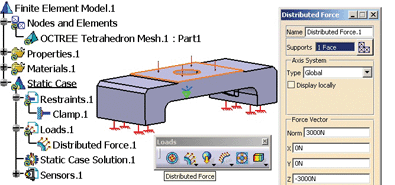
Fig. 4 — The distributed force application.
Now, after the constraints and loading case, the next stage is the analysis computation, launched by pressing the “Compute” icon. As a result, the dialog window with the same name is opened, figure 5, where the user selects the “All” option, followed by the update of the subelement “Static Case Solution”.
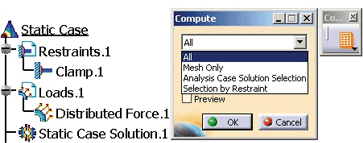
Fig. 5 — Launching the computation.
If the user unchecks the “Preview” option, the analysis time is shortened by not displaying the information window “Computation Resources Estimation”, figure 6.
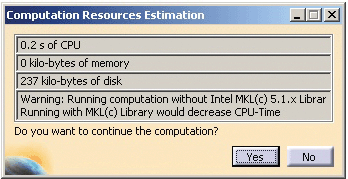
Fig. 6— Computation resource estimation.
However, this window has an important role in very complex analysis processes, because it offers informations about the calculation time and the necessary space on disk.
Once the calculus is finished, the user has at his disposal some tools from the “Image” toolbar to visualize the results. The specification tree is completed with different sub-elements of the inserted images. By default, the last added is the active one, by deactivating the previous others, figure 7.

Fig. 7— The Image toolbar and the list from the specification tree.
This shows the specification tree containing a list of three images (and also results) and their icons, as part of the subelement “Static Case Solution”.Next, evaluate the four image results shown in figures 8-11.
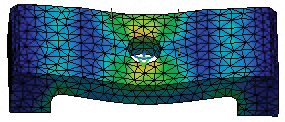
Fig. 8 — The Von Mises Stress result. Note that the deformations are graphically exaggerated to simplify drawing conclusions from this and Fig. 9 images.
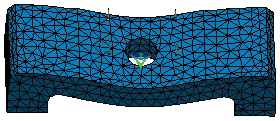
Fig. 9— The Deformed Mesh result.
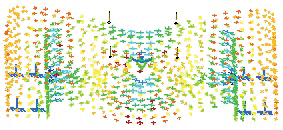
Fig. 10 — The Stress Principal Tensor result.

Fig. 11— The Estimated Error result.
These correspond to the calculations of the mechanical part. Note that the deformations are graphically exaggerated to simplify drawing conclusions from these images.To find the maximum and minimum tensions (stresses) after the analysis, activate the “Von Mises Stress” result and, from the “Analysis Tools” toolbar, applying the “Information” tool, the program opens an information window with the same name, figure 12.
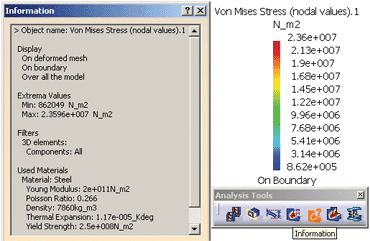
Fig. 12 — The max and minimum values for stresses. At right is the stress palette.
In this figure, the stresses values palette is shown for the “Von Mises Stress” result. The smallest values for the stresses are in the lower section of that palette, and the highest ones in the upper section. Also, these two extreme values are shown in the information window.
After the analysis ends, the user should compare the yield strength value for the chosen material with the maximum value in the “Von Mises Stress” result. The stress value is almost ten times smaller (2.36_107 N/m2 vs 2.5_108 N/m2), so the conclusion can be drawn: the mechanical part resists or withstands the planned loading.
Discuss this article at www.FEA-Forums.com
Filed Under: Software • 3D CAD, Software • FEA, ENGINEERING SOFTWARE




Tell Us What You Think!