One of the electromagnetic principles that governs the operation of an electric motor is Faraday’s law, which states that when the magnetic environment of a coil of wire is changed — whether by moving the magnet and coil relative to each other or by changing the magnetic field — a voltage, or electromotive force (EMF), will be induced.
Another fundamental law of electromagnetism — Lenz’ law — builds on Faraday’s law to ensure that the magnetic flux remains constant. Lenz’ law explains that the polarity of the induced EMF is such that the current it generates (according to Ohm’s law) will have a magnetic field whose direction opposes the change that produced it. In other words, the induced magnetic field opposes the original magnetic field. (Notice the negative sign in the equation for EMF, below.)
![]()
E = induced EMF (V)
N = number of turns in the coil
Φ = magnetic flux (weber, Wb)
t = time (s)
The currents generated according to Faraday’s law are known as eddy currents, because they flow, or circulate, in the conductor — similar to eddies in a body of water. The magnitude of eddy current is directly related to the strength of the magnetic field, the rate of change of the magnetic flux, and the area of the coil, while having an inverse relationship to the resistivity of the conductor.
As eddy currents flow through the conductor, heat is generated, referred to as Joule heating. The amount of Joule heating is proportional to the square of the current, so even a small reduction in eddy currents can have a significant effect on the amount of heat produced.
One of the most effective ways to reduce eddy currents in motors is to use laminations (thin sheets of metal that are electrically insulated from one another), which have a smaller surface area and higher resistance that a solid core. This reduces the magnitude of the eddy currents that can form, and, in turn, the amount of Joule heating that occurs.

Image credit: wikipedia.org
The power lost as a result of Joule heating is referred to as eddy current loss, which can be found with the equation:
![]()
Pe = eddy current loss (W)
ke = eddy current coefficient
B = flux density (Wb/m2)
f = frequency of magnetic reversals per second (Hz)
t = thickness of the conductor (m) *this is why thin laminations are used rather than solid cores
V = volume of the conductor (m3)
Notice that the amount of eddy current loss is proportional to the square of the frequency of magnetic reversals, and therefore, to the square of motor speed. This is why the torque produced by an electric motor decreases as speed increases — because of heating due to eddy current losses (as well as other losses, such as hysteresis losses). Motors with high pole counts, such as stepper motors, experience high eddy current losses due to their high frequency of magnetic reversals.
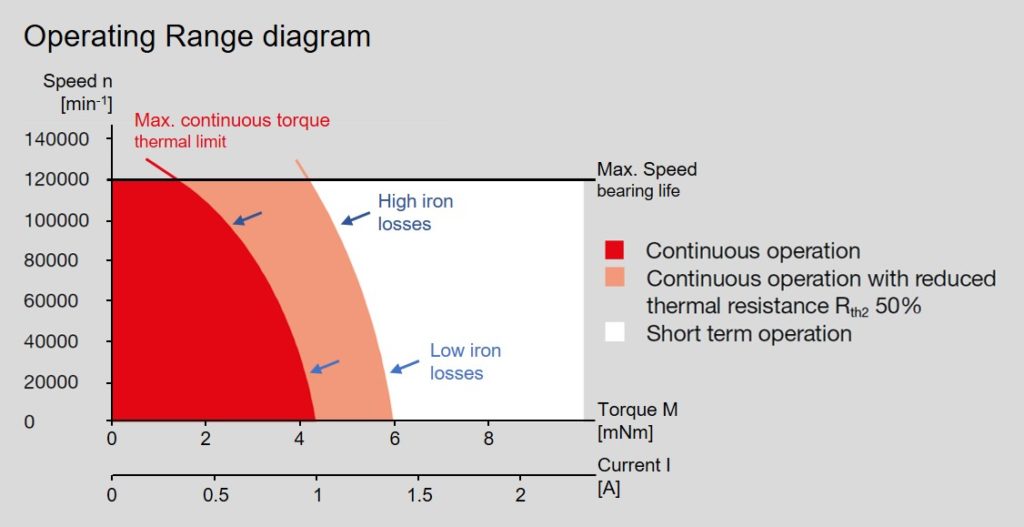
Image credit: maxon
Eddy current losses and hysteresis losses are categorized as core losses (also referred to as iron losses or magnetic losses) because they depend on the magnetic paths through the iron core of the motor.
Although eddy currents are an undesirable occurrence in electric motors, they are useful in other applications, such as eddy current brakes, non-destructive testing devices, and inductive proximity sensors.
Filed Under: Motion Control Tips




