Resonance occurs when the resonant frequency (also referred to as the natural frequency) of an object or system is equal or very close to the frequency at which it is being excited. This causes the object or system to vibrate strongly and can result in unexpected – and sometimes catastrophic – behavior.
When one oscillating object or system (a piezo drive or controller) drives another system (a piezo motor or actuator) at or near the natural frequency of the second system, the second system will oscillate at a high amplitude at a specific frequency. When damping effects are small, the resonant frequency of the system is approximately equal to its natural frequency.
![]()
Where:
f0 = resonant frequency (without load) (Hz)
kT = piezo stiffness (N/m)
meff = effective mass (kg)
The resonant frequency of a piezo motor or actuator depends on its material composition, shape, and volume. For example, a thicker piezo element will have a lower resonant frequency than a thinner element of the same shape. In addition, attaching a load to a piezo motor or actuator reduces its resonant frequency – the higher the load, the more the resonant frequency is reduced. In manufacturer specifications, the resonant frequency given for a piezo actuator assumes that it is unloaded and one end is fixed or attached to a mass that is significantly larger than the actuator.
![]()
Where:
f0‘ = resonant frequency with added mass (Hz)
m´eff = meff + additional mass (kg)
In an electrical circuit representing the piezo element, the frequency at which the impedance of the circuit is at a minimum is the series resonant frequency, fs. Conversely, the parallel resonant frequency, fp, in the equivalent circuit occurs when impedance in the circuit is theoretically infinite (assuming mechanical losses are ignored). This is also known as the anti-resonant frequency, fa.
The series and parallel frequencies are suitable approximations of the minimum and maximum impedance frequencies – fm and fn, respectively – and therefore are used to determine the parameters of the piezoelectric motor or system. Maximum response of a piezo system occurs between fm and fn. Piezo systems with a higher resonant frequency will have a better phase and amplitude response, which means that the operating frequency can be higher.
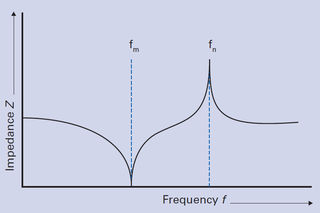
Minimum impedance (fm) occurs at the resonant frequency and maximum impedance (fn) occurs at the anti-resonant frequency.
Image credit: PI Ceramic GmbH
Theoretically, the resonant frequency is the operating frequency at which the piezo material vibrates most readily and converts electrical energy into mechanical energy most efficiently. However, piezo systems (especially actuators used for positioning) are often operated below their resonant frequencies in order to minimize the phase shift between the driving signal and the actuator.
When operated below their resonant frequencies, piezo actuators act like capacitors, with displacement being proportional to the stored charge. With a rapid increase in control voltage, a piezo system can typically reach its nominal displacement in 1/3 the period of its resonant frequency. However, this causes large overshoot, which must be compensated for by the controller.
![]()
Where:
tmin = minimum rise time (s)
f0 = resonant frequency (Hz)
Feature image credit: Stack Exchange Inc.
Filed Under: Capacitors, Motion control • motor controls, Motion Control Tips




There is an error in the above graph of impedance and frequency. fm is at the antiresonant frequency and fn is at the resonant frequency.