When analyzing electrical circuits — including those for AC induction motors and DC motors — if the circuit contains two or more of the same passive elements (such as resistors) and is wired exclusively in series or exclusively in parallel, the circuit can be drawn with a simpler representation that contains the voltage source and a single, equivalent passive element. This simplified version retains the electrical characteristics of the original circuit and is referred to as an equivalent circuit.
Passive elements are those that dissipate, store, or release energy in the form of voltage or current. Examples of passive elements are resistors, capacitors, and coils (aka inductors).
Active elements deliver or produce energy in the form of voltage or current. They include semiconductor components such as diodes, transistors (field-effect transistors, or FETs, and metal-oxide-semiconductor FETs, or MOSFETs).
The rules for combining resistors to create an equivalent circuit are based on Ohm’s law together with Kirchhoff’s circuit laws.
The first of Kirchhoff’s laws, referred to as Kirchhoff’s current law (KCL), states that the amount of current flowing into any node (junction) in a closed circuit equals the amount of current flowing out of that node, thus ensuring the conservation of charge in a closed circuit.
Kirchhoff’s second law, referred to as Kirchhoff’s voltage law (KVL), states that for a closed circuit, the algebraic sum of all the voltages around the circuit equals zero. Kirchhoff’s voltage law ensures conservation of energy in a closed circuit.
Finding equivalent resistance for series circuits
For a circuit wired in series, Kirchhoff’s voltage law, KVL, tells us that the voltage around the circuit will equal zero. This means the sum of the voltage drops across each resistor will equal the supply voltage. For a series circuit with three resistors, the supply voltage, Vs, equals the sum of the voltages across the three resistors (VR1, VR2, and VR3):
![]()
We know from Kirchhoff’s current law, KCL, that the charge flowing into any node equals the charge flowing out of that node. Series circuits have only one node (junction), so current is the same at all points in the circuit. This means the same current flows across each resistor. Using Ohm’s law, V = IR, to express the voltage across each resistor, we can rewrite the equation above:
![]()
![]()
Now we can see that the equivalent resistance is simply the sum of all the resistances in the series circuit.
![]()
And voltage can now be written in terms of the equivalent resistance.
![]()
The example below shows a series circuit with three resistors.
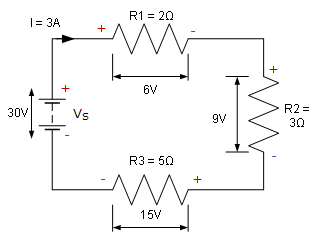
For this circuit, the equivalent resistance is:
![]()
![]()
So the equivalent circuit will have one, 10-ohm equivalent resistor (Req).
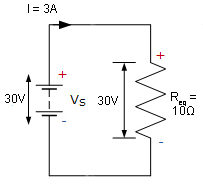
We can check our equivalent circuit by calculating the voltage across the equivalent resistor and ensuring it equals the supply voltage:
![]()
Finding equivalent resistance for parallel circuits
For circuits wired in parallel, we can treat each loop as a separate circuit that is wired in series. Kirchhoff’s voltage law, KVL, tells us that in each separate loops (series circuit), the voltage drop across the resistor equals the supply voltage. For a parallel circuit with three resistors, the voltage drop across each resistor equals the supply voltage.
![]()
![]()
![]()
According to Kirchhoff’s current law, KCL, the current is divided at each node, or junction, such that:
![]() Expressing current as voltage divided by resistance (V/R), according to Ohm’s law:
Expressing current as voltage divided by resistance (V/R), according to Ohm’s law:
![]()
![]()
Rearranging in terms of voltage, we get:
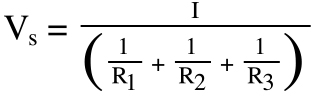
Now the equivalent resistance can be defined as:
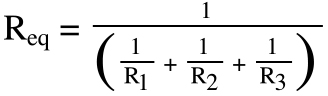
Or:
![]()
In other words, for a parallel circuit, the equivalent resistance is found by adding the reciprocals of the individual resistance values, and then taking the reciprocal of the total.
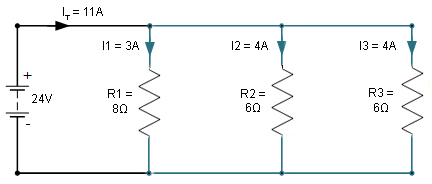
In this parallel circuit with three resistors, the equivalent resistance is:
![]()
![]()
![]()
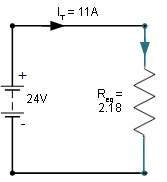
Again, we can check our equivalent circuit by ensuring the voltage across the equivalent resistor equals the supply voltage:
![]()
Kirchhoff’s circuit laws applied to series circuits: For a circuit wired in series, the voltage flowing through the circuit is divided among the passive elements, but the current is the same through each passive element.
Kirchhoff’s circuit laws applied to parallel circuits: For a circuit wired in parallel, the voltage flowing through the circuit is the same across each passive element, but the current is divided among the passive elements.
Filed Under: Motion Control Tips




