Three types of systems are commonly used in mobile applications.  This article provides a simple comparison of constant-flow (CF), constant-pressure (CP), and load-sensing (LS) systems.

A Constant-flow system uses a fixed-displacement pump to provide a constant flow to the system. When the operator requests a portion of the flow to perform a function, a constant-flow system brings the entire flow up to relief-valve pressure. In the valve, the flow is split so that part of the flow goes to move the load and the rest of the flow is sent through an orifice and back to the reservoir. The portion of the flow that goes through the orifice takes a pressure drop from the load pressure to the tank pressure, producing heat.

Major reasons for choosing a CF system include economic viability, ease of maintenance and troubleshooting, and lower maximum system pressures.  CF hydraulic systems are well suited for trucks, some forestry equipment, cranes, and tractors.

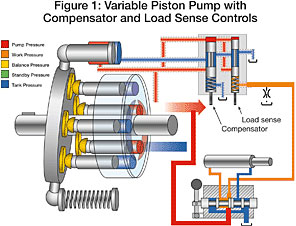
Variable-piston pump with load-sense controls gives the system the flow requested by the operator at the pressure the system requires.

A Constant-pressure system uses a variable-displacement pump with a pressure compensator control to provide the exact flow needed for system operation.  The flow is pressurized at the setting of the compensator control even though the load may not require that much pressure.  When the operator requests flow to move the load, an orificed connection is made in the control valve between the pump and the actuator (motor or cylinder). The pump delivers the flow that the orifice size dictates, but delivers the flow at the compensator pressure setting. As the flow passes though the control orifice, it takes a pressure drop from system pressure to load pressure. This portion of the energy transferred through the system is wasted and produces heat.

A strong benefit of selecting a CP system is that controls respond quickly because the system is always pressurized, delivering instant system pressure upon request.  Other types of systems have to build pressure when controls are activated. High system pressures are available and the pump is the only component in the system that is complex — the control valve is still a relatively simple technology. CP systems are widely used on equipment for railroad repair, oil field applications, and some forestry equipment.

Load-sense system with a variable-displacement pump is designed to give the system the amount of flow requested by the operator at the pressure the system requires to overcome the resistance of the load — plus a small amount of additional pressure that is used to control the system and overcome internal resistance as shown in the schematic.

The load-sense system is the least common and the least understood system of the three, but offers a potential for efficient use of energy.  Currently, load sense systems are the most expensive and the most complicated of the three systems.  They are also the most difficult to troubleshoot — significant training of service technicians is required to help them handle repair and maintenance issues.  However, because both return on investment and energy efficiency are better with these systems, their applications are increasing.

Load-sense system is 50% efficient at a very low pressure of 200 psi, regardless of the flow usage rate. When a more usable pressure of 1000 psi is reached, the LS is over 80% efficient.

Comparing the systems
The first step is understanding the power needed to produce the flow and pressure for each system function, as distinct from the power actually required to move the load.

CF (constant flow) system efficiency is proportional to the percentage of the total flow that is used to move the load. In other words, if 25% of the flow is used, the system is 25% efficient. If 50% of the available flow is used, then the system is 50% efficient.

CP (constant pressure) system efficiency is proportional to the percentage of the total pressure that is used to move the load. In other words, if 25% of the pressure is used, the system is 25% efficient. If 50% of the available pressure is used, then the system is 50% efficient.

The LS (load sense) system is also controlled by pressure like the CP system, but not in direct proportion, which usually results in a more efficient system.

The easiest way to compare these systems is to graph their performance in a sample system. In the sample system, the pump has a maximum flow rate of 20 gpm and the system pressure control is set at 4000 psi. The LS system has a control pressure of 200 psi.

Load sense vs. constant flow — As the graph shows, the LS system is 50% efficient at a very low pressure of 200 psi, regardless of the flow usage rate. When a more usable pressure of 1000 psi is reached, the LS is over 80% efficient across the spectrum of system flow-usage rates.  The CF system, as shown, does not reach 80% efficiency until a flow-usage rate of 16 gpm or above is achieved. This gives the LS system a big efficiency advantage over the CF system, especially in higher pressure and low-to-medium flow situations.

Load sense vs. constant pressure — As shown in the second graph, the LS system provides better efficiency than the CP system at all pressures up to 3800 psi.  This is because pressure does not control the LS system proportionately as it does in the CP system.

Load-Sense system provides better efficiency than the CP system at all pressures up to 3800 psi.

Low-pressure standby
These three systems also vary in power (hp) usage during low-pressure standby. A system is in standby when it is running, but no work demand is placed on it.

CF system in standby sends its flow from the pump through the valve and back to the reservoir.  A pressure drop of 100 psi is a realistic characteristic of this type of system. In our example above, during standby, the CF converts 1.2 Hp (20 gpm x 100 psi x .000583) to heat.

Constant-pressure system is least efficient during standby, converting the highest percentage of driving power to heat. 

CP system remains at full system pressure during standby. As illustrated in our example, full system pressure is 4000 psi. During this time, the pump leakage flow is subjected to full pressure and takes a pressure drop as it travels back to reservoir. A realistic leakage flow for a 20-gpm pump at 4000 psi is 1.5 gpm. So this CP system, during standby, converts 3.5 Hp (1.5 gpm x 4000 psi x .000583) to heat.

LS system at low-pressure standby in our example is at 200 psi. At standby, the pump leakage flow is subjected to control pressure and takes a pressure drop as it travels back to reservoir. A realistic leakage flow for a 20-gpm pump at 200 psi is 0.75 gpm. So the LS system converts 0.1 Hp (0.75 gpm x 200 psi x .000583) to heat, which is significantly less than the other two systems.

To eliminate standby power usage in mobile hydraulic system applications such as those on trucks, we recommend installing a PTO (power take off) or an electric clutch to disengage the pump from the engine when the system is not in use.